拜占庭将军问题(The Byzantine Generals Problem)提供了对分布式共识问题的一种情景化描述, 由 Leslie Lamport 等人在1982年首次发表. 论文同时提供了两种解决拜占庭将军问题的算法:
- 口信消息型解决方案(A solution with oral message);
- 签名消息型解决方案(A solution with signed message).
本文之后将详细讲述这两种算法. 事实上, 拜占庭将军问题是分布式系统领域最复杂的容错模型, 它描述了如何在存在恶意行为(如消息篡改或伪造)的情况下使分布式系统达成一致. 是我们理解分布式一致性协议和算法的重要基础.
拜占庭将军问题描述
拜占庭将军问题描述了这样一个场景:
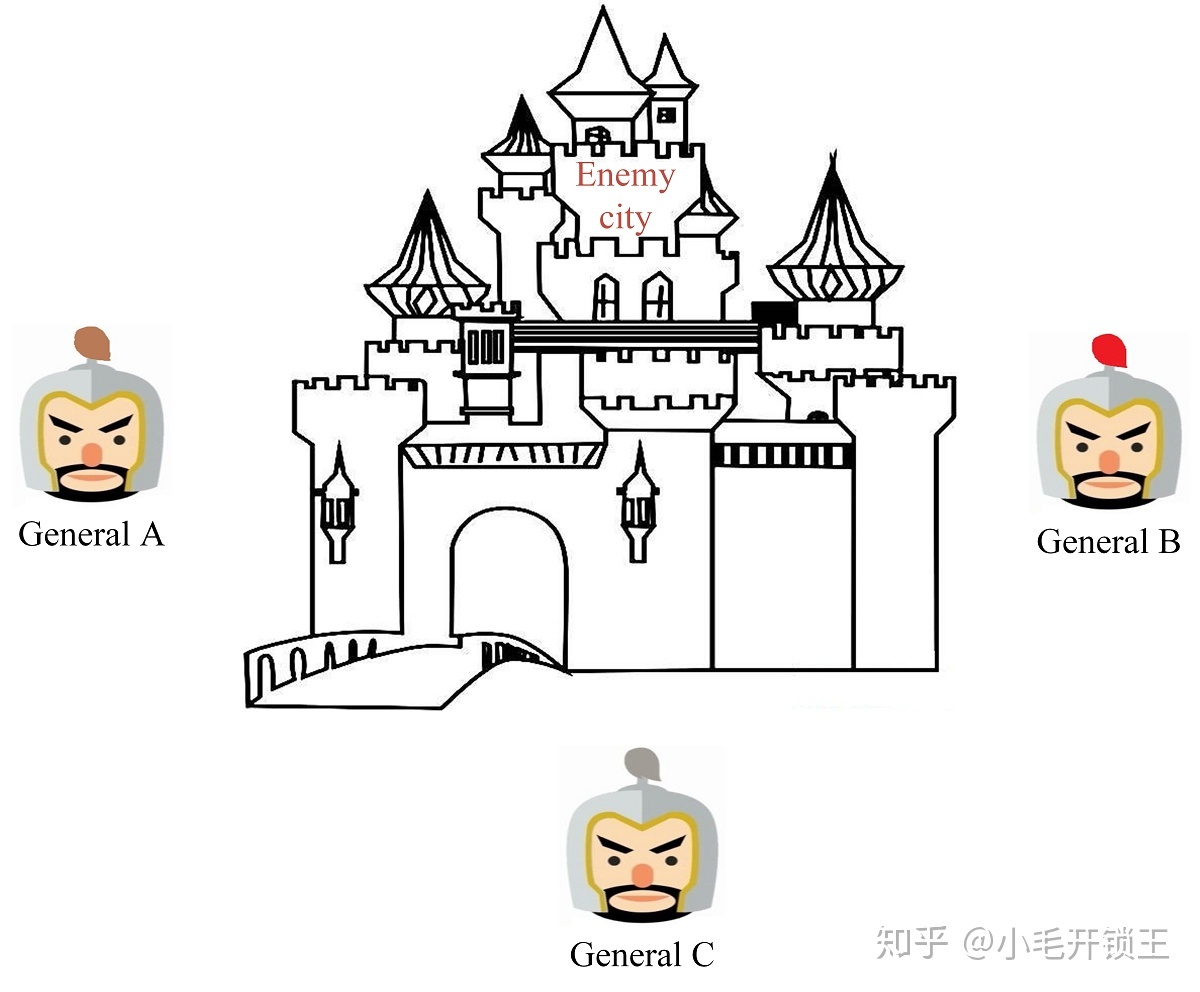
拜占庭帝国(Byzantine Empire) 军队的几个师驻扎在敌城外, 每个师都由各自的将军指挥. 将军们只能通过信使相互沟通. 在观察敌情之后, 他们必须制定一个共同的行动计划, 如进攻(Attack)或者撤退(Retreat), 且只有当半数以上的将军共同发起进攻时才能取得胜利. 然而, 其中一些将军可能是叛徒, 试图阻止忠诚的将军达成一致的行动计划. 更糟糕的是, 负责消息传递的信使也可能是叛徒, 他们可能篡改或伪造消息, 也可能使得消息丢失.
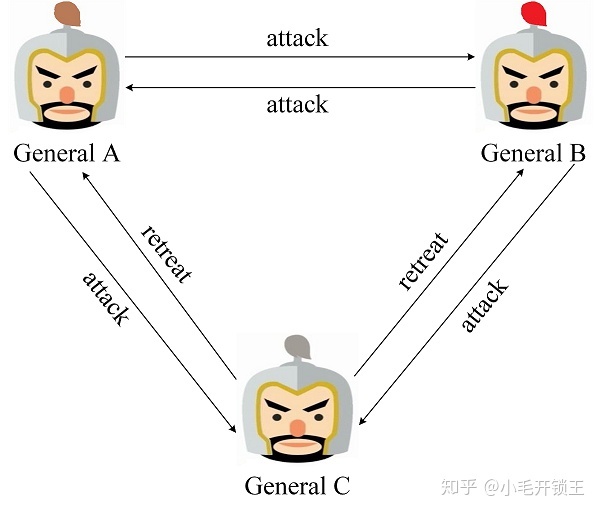
为了更加深入的理解拜占庭将军问题, 我们以三将军问题为例进行说明. 当三个将军都忠诚时, 可以通过投票确定一致的行动方案, 图2展示了一种场景, 即 General A, B 通过观察敌军军情并结合自身情况判断可以发起攻击, 而 General C 通过观察敌军军情并结合自身情况判断应当撤退. 最终三个将军经过投票表决得到结果为进攻:撤退=2:1, 所以将一同发起进攻取得胜利. 对于三个将军, 每个将军都能执行两种决策(进攻或撤退)的情况下, 共存在 6 中不同的场景, 图 2 是其中一种, 对于其他 5 中场景可简单地推得, 通过投票三个将军都将达成一致的行动计划.
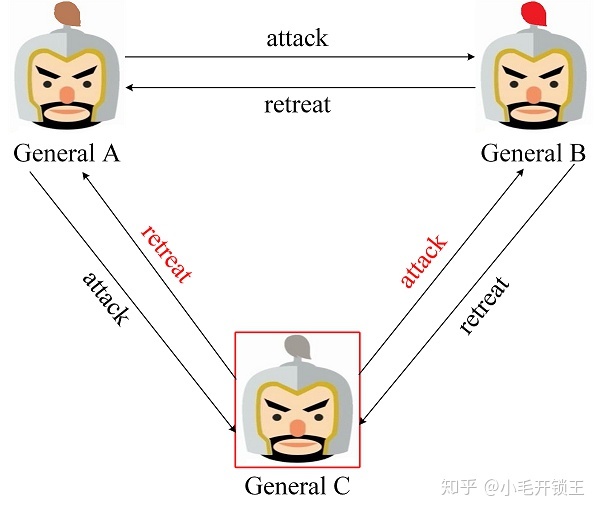
当三个将军中存在一个叛徒时, 将可能扰乱正常的作战计划. 图3展示了 General C 为叛徒的一种场景, 他给 General A 和 General B 发送了不同的消息, 在这种场景下 General A 通过投票得到进攻:撤退=1:2, 最终将作出撤退的行动计划; General B 通过投票得到进攻:撤退=2:1, 最终将作出进攻的行动计划. 结果只有 General B 发起了进攻并战败.
事实上, 对于三个将军中存在一个叛徒的场景, 想要总能达到一致的行动方案是不可能的. 详细的证明可参看 Leslie Lamport 的论文. 此外, 论文中给出了一个更加普适的结论: 如果存在_m_个叛将, 那么至少需要_3m+1_个将军, 才能最终达到一致的行动方案.
解决方案
Leslie Lamport 在论文中给出了两种拜占庭将军问题的解决方案, 即口信消息型解决方案(A solution with oral message)和签名消息型解决方案(A solution with signed message).
口信消息型解决方案
首先, 对于口信消息(Oral message)的定义如下:
- A1. 任何已经发送的消息都将被正确传达;
- A2. 消息的接收者知道是谁发送了消息;
- A3. 消息的缺席可以被检测.
基于口信消息的定义, 我们可以知道, 口信消息不能被篡改但是可以被伪造. 基于对图 3 场景的推导, 我们知道存在一个叛将时, 必须再增加 3 个忠将才能达到最终的行动一致. 为加深理解, 我们将利用 3 个忠将 1 个叛将的场景对口信消息型解决方案进行推导. 在口信消息型解决方案中, 首先发送消息的将军称为指挥官, 其余将军称为副官. 对于 3 忠 1 叛的场景需要进行两轮作战信息协商, 如果没有收到作战信息那么默认撤退. 图 4 是指挥官为忠将的场景, 在第一轮作战信息协商中, 指挥官向 3 位副官发送了进攻的消息; 在第二轮中, 三位副官再次进行作战信息协商, 由于 General A, B 为忠将, 因此他们根据指挥官的消息向另外两位副官发送了进攻的消息, 而 General C 为叛将, 为了扰乱作战计划, 他向另外两位副官发送了撤退的消息. 最终 Commanding General, General A 和 B 达成了一致的进攻计划, 可以取得胜利.
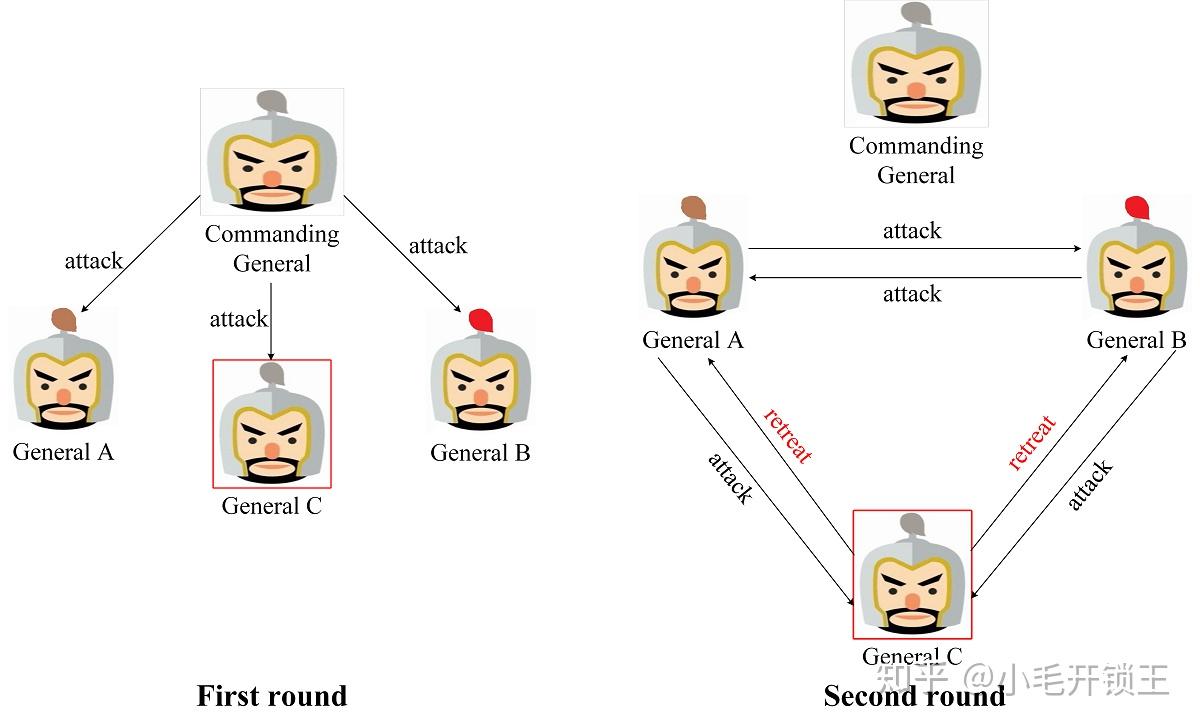
图 5 是指挥官为叛将的场景, 在第一轮作战信息协商中, 指挥官向 General A, B 发送了撤退的消息, 但是为了扰乱 General C 的决定向其发送了进攻的消息. 在第二轮中, 由于所有副官均为忠将, 因此都将来自指挥官的消息正确地发送给其余两位副官. 最终所有忠将都能达成一致撤退的计划.
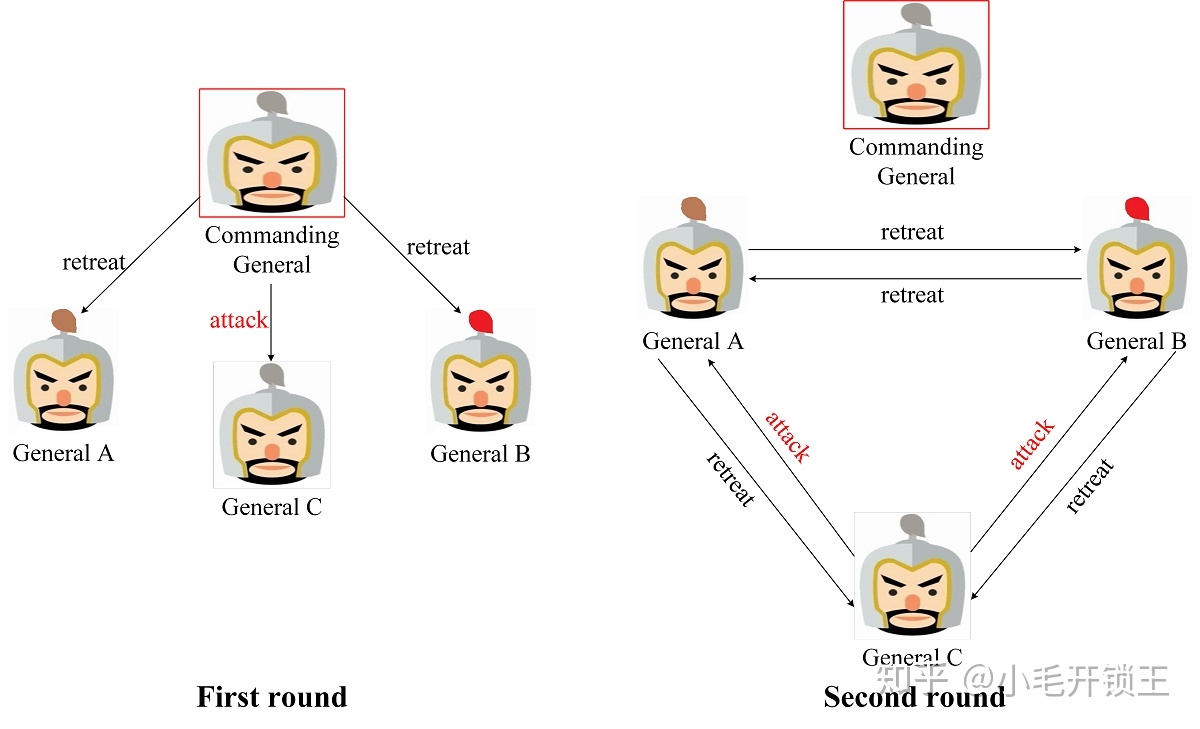
如上所述, 对于口信消息型拜占庭将军问题, 如果叛将人数为_m_, 将军人数不少于_3m+1_, 那么最终能达成一致的行动计划. 值的注意的是, 在这个算法中, 叛将人数_m_是已知的, 且叛将人数_m_决定了递归的次数, 即叛将数_m_决定了进行作战信息协商的轮数, 如果存在_m_个叛将, 则需要进行_m+1_轮作战信息协商. 这也是上述存在 1 个叛将时需要进行两轮作战信息协商的原因.
签名消息型解决方案
同样, 对签名消息的定义是在口信消息定义的基础上增加了如下两条:
- A4. 忠诚将军的签名无法伪造,而且对他签名消息的内容进行任何更改都会被发现;
- A5. 任何人都能验证将军签名的真伪.
基于签名消息的定义, 我们可以知道, 签名消息无法被伪造或者篡改. 为了深入理解签名消息型解决方案, 我们同样以 3 三将军问题为例进行推导. 图 6 是忠将率先发起作战协商的场景, General A 率先向 General B, C 发送了进攻消息, 一旦叛将 General C 篡改了来自 General A 的消息, 那么 General B 将将发现作战信息被 General C 篡改, General B 将执行 General A 发送的消息.
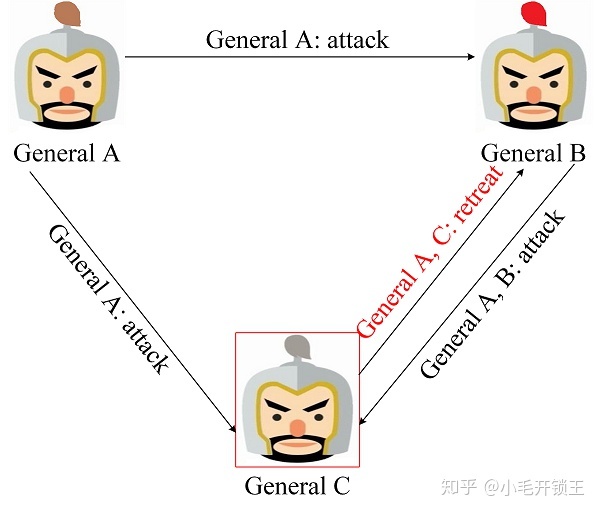
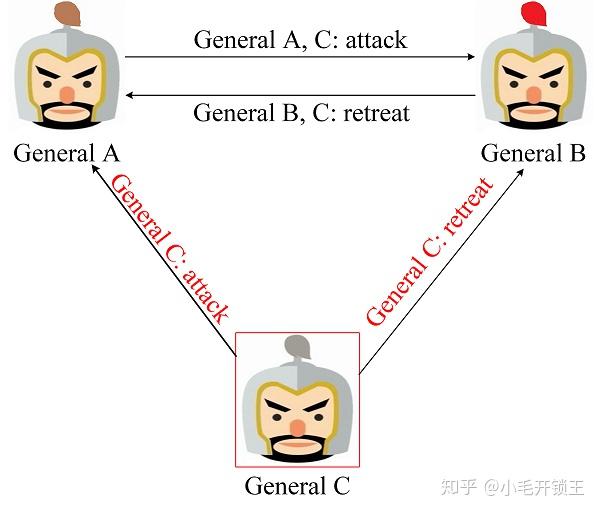
图 7 是叛将率先发起作战协商的场景, 叛将 General C 率先发送了误导的作战信息, 那么 General A, B 将发现 General C 发送的作战信息不一致, 因此判定其为叛将. 可对其进行处理后再进行作战信息协商.
签名消息型解决方案可以处理任何数量叛将的场景.
论文简介
Leslie Lamport 等人的论文_‘The Byzantine Generals Problem’_ 的提纲如下:
- Introduction: 介绍了拜占庭将军问题;
- Impossibility Results: 通过反正法证明了, 三将军问题对于口信消息是无解的;
- A solution with oral message: 介绍了口信消息型拜占庭将军问题的解决方案;
- A solution with signed message: 介绍了签名消息型拜占庭将军问题的解决方案;
- Missing communication paths: 讲述了在通信小时情况下的拜占庭将军问题;
- Reliable systems: 讲述了如何通过拜占庭将军问题构建可靠的系统;
- Conclution: 总结.
总结
在分布式系统领域, 拜占庭将军问题中的角色与计算机世界的对应关系如下:
- 将军, 对应计算机节点;
- 忠诚的将军, 对应运行良好的计算机节点;
- 叛变的将军, 被非法控制的计算机节点;
- 信使被杀, 通信故障使得消息丢失;
- 信使被间谍替换, 通信被攻击, 攻击者篡改或伪造信息.
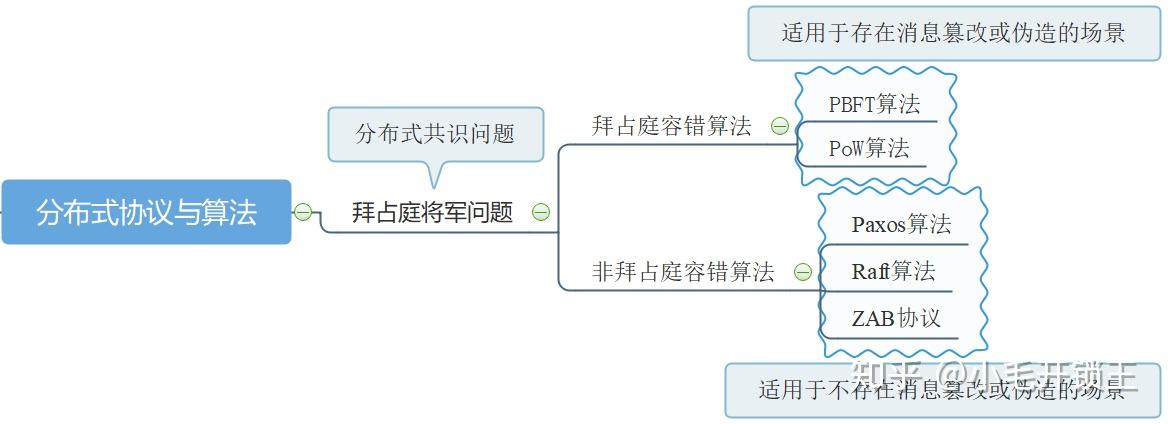
如上文所述, 拜占庭将军问题提供了对分布式共识问题的一种情景化描述, 是分布式系统领域最复杂的模型. 此外, 它也为我们理解和分类现有的众多分布式一致性协议和算法提供了框架. 现有的分布式一致性协议和算法主要可分为两类:
- 一类是故障容错算法(Crash Fault Tolerance, CFT), 即非拜占庭容错算法, 解决的是分布式系统中存在故障, 但不存在恶意攻击的场景下的共识问题. 也就是说, 在该场景下可能存在消息丢失, 消息重复, 但不存在消息被篡改或伪造的场景. 一般用于局域网场景下的分布式系统, 如分布式数据库. 属于此类的常见算法有 Paxos 算法, Raft 算法, ZAB 协议等.
- 一类是拜占庭容错算法, 可以解决分布式系统中既存在故障, 又存在恶意攻击场景下的共识问题. 一般用于互联网场景下的分布式系统, 如在数字货币的区块链技术中. 属于此类的常见算法有 PBFT 算法, PoW 算法.