第一章 0 的故事
为什么 是 1 ?
这里的逻辑是。
10^3 = 1000
10^2 = 100
10^1 = 10
10^0 = 1
依次除以 10 。
而不是传统意义上的 n 个相乘的概念。
0 起到什么作用?
- 按位计数法中的占位
- 统一标准,简化规则
- 可以在 n == 0 时, 表示 , 而不用对 特殊操作。
- 表示没有。
- 比如没有计划的计划
- 没有药效的药。
第二章 逻辑 - 真与假的二元世界
- 文式图
- 卡诺图
undefined
无论什么遇到 undefined 都返回 undefined
第三章 余数 — 周期性分组
奇偶校验位 ( parity bit )
8 位棋子,令黑棋一定为偶数个。
之后观众的动作
- 翻转白棋 - 黑棋增加, 变成奇数个
- 翻转黑棋 - 黑棋减少, 变成奇数个
- 不翻转棋子。黑棋仍然是偶数个。
寻找恋人
铺设草席
哥尼斯堡七桥
把陆地当作点,桥当作边。然后简化问题。发现问题被归为图论。
将点分为奇点和偶点。
如果可以一笔走完,分为两者情况
- 起点和终点相同 - 所有的点都是偶数点
- 起点和终点不同 - 起点和奇点为奇数,剩余所有都为偶数。
然后统计图中的点的类型,就知道所有的点。
第四章 数学归纳法 - 循环
断言对于 0 以上的所有整数 n 都成立的方法。
高斯求和法 - 1 次加法 + 1 次乘法 + 1 次除法
第五章 排列组合
加法法则:
在集合中没有重复元素时成立。将两个无重复集合的 A、B、想加。
乘法法则:
分别有。
置换:
将 n 个事物按照顺序进行排列 ( 这里 n 个事物都是一样的,所以又代表 重复度 )
排列:
从 n 个事物中抽取出 m 个进行排列
组合:
从 n 个事物中取出 m 个, 并不考虑顺序。
组合 = 排列/置换
注 : 我认为这里这个重复度的概念非常重要。
第六章 递归
汉诺塔问题
H(n) = H(n-1) + 1 + H(n-1);
解出 n 层汉诺塔的移动次数 = 解出 n-1 层 + 移动最大圆盘 + 解出 n-1 层
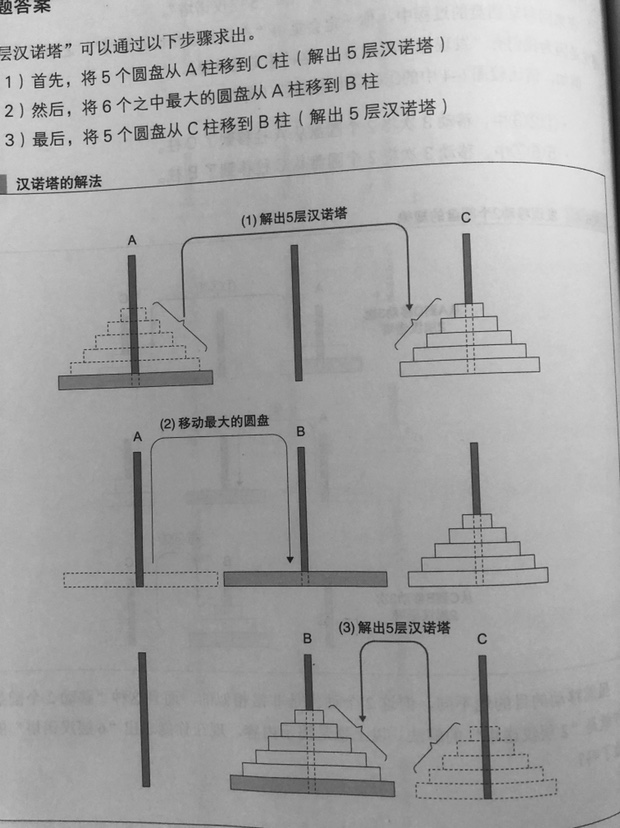
相关例子:
- 阶乘
- 帕斯卡三角形
帕斯卡三角形 - 组合数
- 代表两数相加之和。
- 代表到达某分叉点的情况数。
- 从 n 张中选出 k 张的组合 = 选择特定牌的组合 + 不选定特定牌的组合
分型图 - 含有递归结构的图
比如 谢尔平斯基三角形
第七章 指数爆炸
- 二分查找
- 通过每次取 1/2 来简化计算
- 对数简化
- 指数级问题在对数层面只是线性的
第八章 不可解问题
反证法
可数
集合的元素时有限的,活着集合中的所有元素都与正整数一一对应。
无限集合中,可数的意思: 可按一定规律既无 “遗漏” 也无 “重复” 的数出来。
有理数 :
无限不循环小数不是有理数
有理数通过排序可以证明可数。
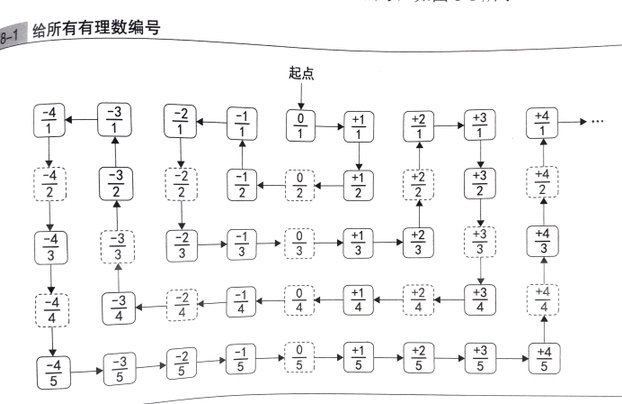
对角论证法
- 所有整数数列的集合是不可数的
- 所有实数的集合也是不可数的
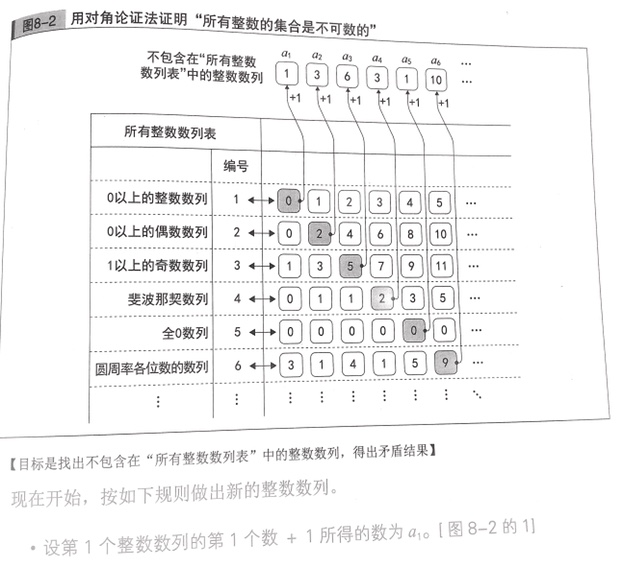
不可解问题:
写一个程序判断如果随机给定一个程序以及输入,这个程序是否会宕机。